Homeomorphisms and topological embeddings

Overview §

Recall the definition of a continuous function between topological spaces.

Definition: Continuous function in topological space

Let $X,Y$ be topological spaces. A function $f:X\to Y$ is continuous if for every open subset $V\subset Y$, the preimage set $f^{-1}(V)$ is an open subset of $X$.

Link to original

A homeomorphism is a “bijective correspondence” between collections of open sets in different topological spaces; that is, a function that is continuous, bijective, and has a continuous inverse.

Definition: Homeomorphism, homeomorphic

A function between topological spaces $f:X\to Y$ is a homeomorphism if $f$ is continuous, bijective, and its inverse $f^{-1}:X\to Y$ is continuous.

$X,Y$ are homeomorphic if there exists a homeomorphism between them, and we write $X\cong Y$. Equivalently, we have $X\cong Y$ if there exists continuous functions $f:X\to Y$, $g:Y\to X$ such that $g\circ f={\text{id}}_X$ and $f\circ g={\text{id}}_Y$.

Crucially, since homeomorphisms give correspondences between collections of open sets in topological spaces, any topological property on one space (i.e., a property that can be entirely expressed in terms of the topology on the space) can be used to express the corresponding property on another, homeomorphic space.

Homeomorphisms, which preserve topological structure, are analogous to isomorphisms in algebra, which are bijective correspondences that preserve algebraic structure. However, while a isomorphism—or bijective homomorphism—in algebra is guaranteed to have an inverse that is also a homomorphism, a continuous function in topology is NOT guaranteed to have a continuous inverse.

---

Ways to show (non-)homeomorphisms §

• Removing cut points. As a consequence of continuous functions preserving (path-)connectedness, if two spaces are homeomorphic and one is (path-)connected, the other is as well. If removing a point disconnects one space but not the other, then they cannot be homeomorphic (e.g., the intervals $[0,1],(0,1),[0,1)$).

• Explicitly construct bijection

• Use the fact that f continuous, X compact, and Y hausdorff

• Induce one with the quotient map (similar to above)

---

Embeddings §

Definition: Topological embedding

A function between topological spaces $f:X\to Y$ is an embedding if it is continuous, injective, and the restriction of its range to the image of $f$, the function $f’:X\to f(X)$ defined by $x\mapsto f(x)$ is a homeomorphism.

---

Examples of homeomorphisms §

#wip See homeworks, $\{x\}\times Y\cong Y$.

• 3.4 – ${\mathbb{R}}^n\backslash \{0\}\cong {\mathbb{R}}_{>0}\times S^{n-1}$ by setting components $f_1(\vec{x})=|\vec{x}|$ and $f_2(\vec{x})=\vec{x}/|\vec{x}|$
• 4.5 – homeomorphism vs. path components?

All open balls and all spheres in ${\mathbb{R}}^n$ are homeomorphic §

Given $x\in {\mathbb{R}}^n$, the open ball of radius $ϵ$ centered at $x$ is the set

$$B(x,ϵ)=\{y\in {\mathbb{R}}^n||x-y|<ϵ\},$$

and the corresponding sphere of radius $r$ is the set $S(x,r)=\{y\in {\mathbb{R}}^n||y-x|=r\}$. The claim that all balls are homeomorphic and all spheres are homeomorphic means that for all $x,y\in {\mathbb{R}}^n$, we have $B(x,ϵ)\cong B(y,\delta )$ for $ϵ,\delta >0$ and $S(x,,r)\cong S(y,t)$ for all $r,t>0$.

We can find an explicit bijection between any two balls by moving the ball from $x$ to the origin, scaling by $\delta /ϵ$, and moving the ball to $x$. A bijection between spheres can be taking the complement of each ball in ${\mathbb{R}}^n$, then restricting the previous continuous bijection and it continuous inverse to these new domains. (See Topology Homework 3.4 for full argument.)

Stereographic projections §

We have

$${\mathbb{R}}^n\cong S^n\backslash \{N\}$$

where $N$ is the “north pole” of the the $n+1$ dimensional unit sphere $S^n$. The associated homeomorphism is $\mathbf{i}:{\mathbb{R}}^n\to S^n\backslash \{N\}$ defined by

$$\mathbf{i}(x)=(t(x)x_1,\dots ,t(x)x_n,1-t(x)),t(x)=\frac{1}{1+x_1^2+\cdots +x_n^2},$$

and the inverse is $f:S^n\backslash \{N\}\to {\mathbb{R}}^n$ defined by

$$f(x)=\frac{1}{1-x_{n+1}}(x_1,\cdots ,x_n).$$

🔺 Exercise. Check this is a homeomorphism.

---

Non-examples of homeomorphisms §

Open, half-open, and closed intervals of $\mathbb{R}$ §

Closed intervals are compact, so they are not homeomorphic to either open or half-open intervals. We may delete the endpoint of a half-open interval to obtain an open interval, which is connected, but deleting any point of the open interval will create a disconnected (i.e., one for which there exists a separation).

Unions of line segments in ${\mathbb{R}}^2$ §

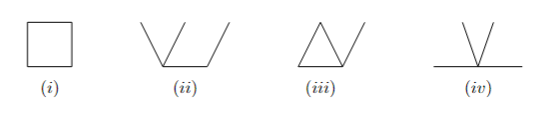
Homeomorphisms induce bijections between (path-)components. These are not homeomorphic because the maximal number of path components created by deleting a point of each space is different for each subspace.

---

Review §

• Is a continuous bijection necessarily a homeomorphism? Give an example.