Real projective space

Overview and basic definition

Definition: Real projective space

Define an equivalence relation $\sim$ on ${\mathbb{R}}^{n+1}\backslash \{\vec{0}\}$ by setting $x\sim y$ if and only if $x,y$ are on the same line through the origin; precisely, this means that there exists $t\in \mathbb{R}\backslash \{0\}$ such that $x=ty$. Then $x$ and $y$ are sometimes said to be antipodal.

The $n$-dimensional real projective space ${\mathbb{RP}}^n={\mathbb{R}}^{n+1}/\sim$ is the “space of lines in ${\mathbb{R}}^{n+1}$.”

---

In point-set topology

• Homeomorphisms and topological embeddings: The real projective space is homeomorphic to the following quotient spaces:
  • $S^n/(x\sim -x)$, the sphere with antipodal points identified;
  • $D^n/\sim$, where where $D^n\subset {\mathbb{R}}^n$ is the closed unit disk centered at the origin and the equivalence classes are given by $x\sim -x$ if $\Vert x\Vert =1$;
  • In the case $n=1$, we have $\mathbb{R}{P}^1\cong S^1$.
• Topological manifolds: The homeomorphisms above imply that $\mathbb{R}{P}^n$ is a topological $n$-manifold, i.e., locally Euclidean, Hausdorff, and second-countable (has a countable basis).

---

In algebraic topology

• Cell attachments and complexes: $\mathbb{R}{P}^n$ has the cell complex structure $e^0\cup e^1\cup \cdots \cup e^n,$ with one cell $e^i$ in each dimension $0\le i\le n$.
• Fundamental group of the circle: Since $\mathbb{R}{P}^1\cong S^1$, we know that it has fundamental group ${\pi }_1(\mathbb{R}{P}^1,x)\cong \mathbb{Z}$.
• Calculating fundamental groups: This theorem can be applied to calculate the fundamental group when $n\ge 2$ by “guessing” a homeomorphism $\mathbb{R}{P}^n\cong S^n/G$, where $G=\mathbb{Z}/2\mathbb{Z}$ is the cyclic group of order 2 whose generator acts on $S^n$ by $x\mapsto -x$. Thus, ${\pi }_1(\mathbb{R}{P}^n)\cong \mathbb{Z}/2\mathbb{Z}$

---

Notes

Homeomorphism with $S^n/(x\sim -x)$

Claim: The real projective space is locally $n$-Euclidean.

Proof from Topology.

For $0\le i\le n$, define the set of equivalence classes

$$U_i=\{[x_0,\dots ,x_n]\in {\mathbb{RP}}^n|x_i\ne 0\}.$$

This is well-defined since if $x_i\ne 0$, then $t{x}_i\ne 0$ for all $t\in \mathbb{R}\backslash \{0\}$. Each $U_i$ is open since

$$q^{-1}(U_i)=\{x\in {\mathbb{R}}^{n+1}|x_i\ne 0\}$$

is open in ${\mathbb{R}}^{n+1}$ (see the following commutative diagram). We will show that $U_i\cong {\mathbb{R}}^n$ for all $i$, then the claim follows from the fact that ${\bigcup }_{i=0}^n{U}_i={\mathbb{RP}}^n$.

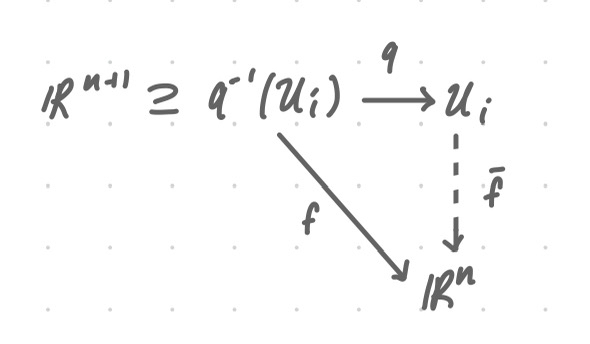
concept-question Why is the vector $n$-dimensional?

wip Define $f:q^{-1}(U_i)\to {\mathbb{R}}^n$ by $f(\mathbf{x})=\mathbf{x}/x_i$ for all $\mathbf{x}=(x_0,\dots ,x_n)$. Note that $f(\mathbf{x})=f(t\mathbf{x})$ since both numerator and denominator will be scaled by $t$, so $f$ induces a map $\bar{f}:U_i\to {\mathbb{R}}^n$ satisfying

$$f(\mathbf{x})=\bar{f}([\mathbf{x}])=\left(\frac{x_0}{x_i},\dots ,\frac{x_{i-1}}{x_i},\frac{x_{i+1}}{x_i},\dots ,\frac{x_n}{x_i}\right).$$

The map $\bar{f}$ is bijective since we can define an explicit inverse

$${\bar{f}}^{-1}([\mathbf{x}])=[(x_0,\dots ,x_{i-1},1,x_{i+1},\dots ,x_n)].$$

As a concrete example, for $n=1$ we have .

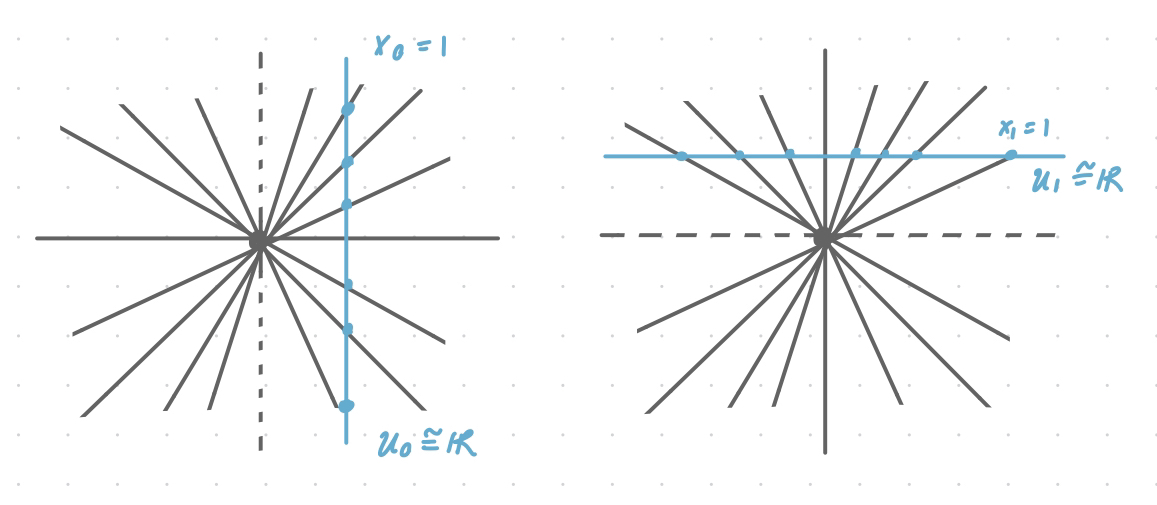As a topological manifold

Theorem ( Topology HW 8.4): The real projective space is homeomorphic to quotients of spheres and closed disks

The real projective space ${\mathbb{RP}}^n$ is homeomorphic to the following quotient spaces:

• (i) $S^n/(x\sim -x)$, the unit sphere in ${\mathbb{R}}^{n+1}$ with antipodal points identified;
• (ii) $D^n/\sim$, where $D^n\subset {\mathbb{R}}^n$ is the closed unit disk centered at the origin and the equivalence classes are given by $x\sim -x$ if $\Vert x\Vert =1$.

Thus, ${\mathbb{RP}}^n$ is a topological n-manifold.

Facts:

• Sn quotient map is open
• Sn Hausdorff.