Lifting properties of covering spaces

Overview and basic definition

Lifting map

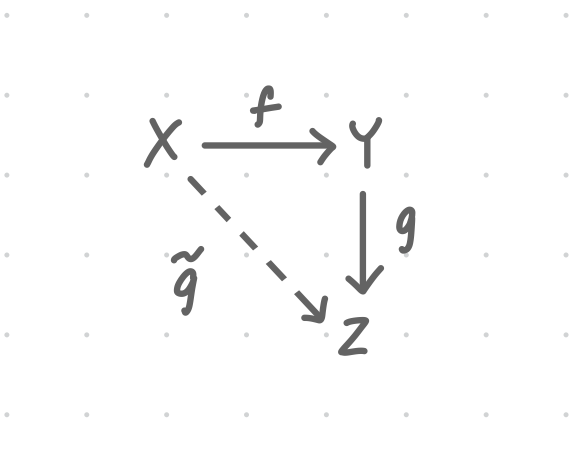
Let $f:X\to Y$ be continuous. If $g:Z\to Y$ is also continuous, then a lift of $g$ is a continuous map $\tilde{g}:Z\to X$ such that $f\circ \tilde{g}=g$.

Covering maps have several special lifting properties:

• Homotopy lifting: A homotopy into the base space has a unique lift to a homotopy into its covering space.
• Lifting criterion: Given some connectivity assumptions on the domain of a continuous map into the base space, a lift of the map exists if and only if the image of its induced homomorphism between fundamental groups is contained in the image of the homomorphism induced by the covering map.
• Unique lifting: Given a map out of a connected covering space, if two lifts agree at one point of the covering, then they agree on all of the covering.

---

Homotopy lifting property

Proof given in the following note: (Theorem) Path and homotopy lifting.

Hatcher 1.30: Lifting homotopies to covering maps

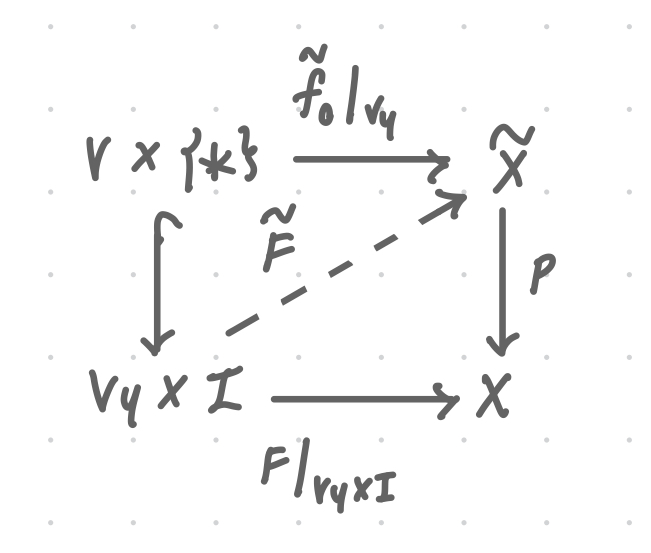
Let $p:\tilde{X}\to X$ be a covering map, $Y$ any other topological space, and $H:Y\times I\to X$ a homotopy. If $f:Y\to \tilde{X}$ is a continuous map such that $H(0,-)=p\circ f$, then there exists a unique homotopy $\tilde{H}:Y\times I\to \tilde{X}$ that lifts $H$, i.e., $p\circ \tilde{H}=H\text{and}\tilde{H}(0,-)=f.$ Moreover, if $H$ is a homotopy relative to a subspace $U\subseteq X$, then so is $\tilde{H}$.

Hatcher 1.31

Let $(X,x_0)$ and $(Y,y_0)$ be based spaces and $p:X\to Y$ be a covering map.

• (i) The induced homomorphism between fundamental groups $p_{\ast }:{\pi }_1(X,x_0)\to p{i}_1(Y,y_0)$ is injective.
• (ii) Let $\delta$ be a loop in $(Y,y_0)$. Then there exists a loop $\gamma$ in $(X,x_0)$ with $\delta =p\circ \gamma$ if and only if the path-homotopy class $[\delta ]\in {\pi }_1(Y,y_0)$ is in the image of $p_{\ast }$.

• Note that this is diff from path lifting because we don’t make assumptions on homotopy class—such a general lift does not necessarily end at $x_0$.

---

Lifting criterion

2025-02-11

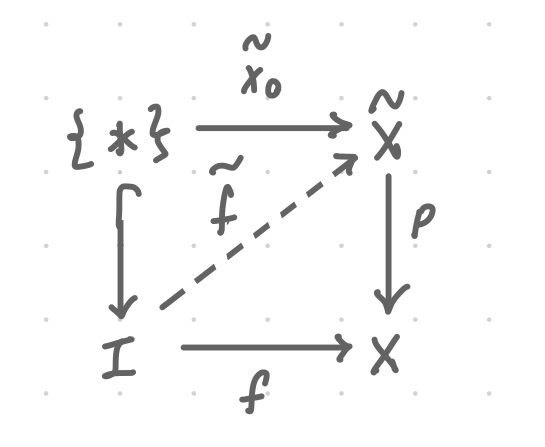
Hatcher 1.33: Lifting criterion for the existence of general lifts

Let $W$ be path-connected and locally path-connected, $f:(W,w_0)\to (X,x_0)$ be continuous, and $p:(Y,y_0)\to (X,x_0)$ be a covering map. Then a unique lift $\tilde{f}:W\to Y$ for which $f=p\circ \tilde{f},\tilde{f}(w_0)=y_0$ exists if and only if the induced homomorphisms satisfy $\text{Im}(f_{\ast })\subseteq \text{Im}(p_{\ast })$, meaning $f_{\ast }([\gamma ])=[f\circ \gamma ]=[p\circ \tilde{f}\circ \gamma ]=p_{\ast }([\tilde{f}\circ \gamma ]).$

---

Unique lifting

Hatcher 1.34: Unique lifting

Let $f:W\to Y$ be continuous and $p:X\to Y$ be a covering map. If $W$ is connected, then whenever two lifts ${\tilde{f}}_1,{\tilde{f}}_2:W\to X$ of $f$ agree at one point of $W$, they also agree on all of $W$.

---

Lifting correspondences

The motivation for a lifting correspondence in (Theorem) The fundamental group of the circle is isomorphic to the additive group of integers is to take a complicated loop in $S^1$ and “unwrap” it by a lift that “straightens out” the loop in $\mathbb{R}$.

Lifting correspondence

Given a covering $p:\tilde{X}\to X$ and some points $x_0\in X$ and ${\tilde{x}}_0\in p^{-1}(x_0)$, define the lifting correspondence $\varphi :{\pi }_1(X,x_0)\to p^{-1}(x_0)$ derived from $p$ as follows: if $f:I\to X$ is a loop at $x_0$ and $\tilde{f}:I\to \tilde{X}$ is a lift starting at ${\tilde{x}}_0$, then

$$\varphi ([f])=\tilde{f}(1)$$

(note that this is a point in $p^{-1}(x_0)$ since $p\circ \tilde{f}(1)=f(1)$).

Munkres 54.4

• (i) If $\tilde{X}$ is path-connected, then $\varphi$ is surjective.
• (ii) If $\tilde{X}$ is simply connected, then $\varphi$ is bijective.

---

Notes

Characterization of homotopy lifting from Topology

Theorem (Munkres 54.1 & 54.2): Unique liftings of paths and path-homotopies in covering spaces

Let $p:\tilde{X}\to X$ be a covering map, $x_0\in X$, and ${\tilde{x}}_0\in p^{-1}(x_0)$. Then:

• (i) Any path $f:I\to X$ starting at $x_0$ has a unique lift to a path $\tilde{f}$ in $\tilde{X}$ starting at ${\tilde{x}}_0$;
• (ii) If $F:I\times I\to X$ is a path-homotopy from two paths $f,g$ which start at $x_0$, then there is a unique lift to a path-homotopy $\tilde{F}:I\times I\to \tilde{X}$ between $\tilde{f},\tilde{g}$, the unique lifts starting at ${\tilde{x}}_0$.

Proof from Topology.

For (i), let $\mathcal{C}$ be a cover of $X$ consisting of sets $U\in \mathcal{C}$ that are each evenly covered by $p$. Then the collection

$$\{f^{-1}(U)|U\in \mathcal{C}\}$$

covers $I$, and since $I$ is compact, we can apply the Lebesgue number lemma (🔺 why?) to find a subdivision

$$0=t_0<t_1<\cdots <t_m=1$$

such that for all $i\in 0,\dots ,m-1$, we have $f([t_i,t_{i+1}])\subseteq U$ for some $U\in \mathcal{C}$.

We now define the lift $\tilde{f}$ incrementally. Begin by setting $\tilde{f}(o)={\tilde{x}}_0$, and suppose $\tilde{f}$ is defined on $[0,t_i$] and we want to define it on $[t_i,t_{i+1}]$. Since $f([t_i,t_{i+1}])\subseteq U$ for some $U$ that is evenly covered by $p$. wip

Note that the previous theorem can be proven as consequences of the more general statement:

Theorem (Hatcher 1.7c):

Given a map $F:Y\times I\to X$ and a map $\tilde{F}:Y\times \{0\}\to \tilde{X}$ lifting the restriction $F{|}_{Y\times \{0\}}$, there is a unique map $\tilde{F}:Y\times I\to \tilde{X}$ lifting $F$ and restricting to the given $\tilde{F}$ on $Y\times \{0\}$.

❓ Question. What is the relationship between the two theorems?

Lifting criterion statement from Hatcher

Theorem: Lifting criterion

Let $Y$ be path-connected and locally path-connected. Given a covering map $p:(\tilde{X},{\tilde{x}}_0)\to (X,x_0)$ and any map $f:(Y,y_0)\to (X,x_0)$, a lift $\tilde{f}:(Y,y_0)\to (\tilde{X},{\tilde{x}}_0)$ exists if and only if the induced homomorphisms satisfy $f_{\ast }({\pi }_1(Y,y_0))\subset p_{\ast }({\pi }_1(\tilde{X},{\tilde{x}}_0)).$