Overview and statement of the theorems
Path lifting
Let be a covering map, a path and let be such that . Then there exists precisely one path such that and .
Homotopy lifting
Let be a covering map, any topological space and be a homotopy. Let be such that . Then there exists precisely one homotopy with and .
Proofs from Algebraic Topology.
Proof of path lifting
Link to originalPath lifting
Let be a covering map, a path and let be such that . Then there exists precisely one path such that and .
Claim 1: The path and homotopy lifting theorems hold when is a trivial covering map, i.e., the preimage is a disjoint union of copies of .
Claim 2: The theorems hold when the image is evenly covered.
Claim 3: Given the assumptions of the homotopy lifting theorem, let be subinterval such that is evenly covered, and be a map such that . Then there exists precisely one map with both
Claim 4: Let be an open cover of . Then there exists such that for each , there is an open subset such that . In other words, is a Lebesgue number for the covering.
Proof. Since is a covering, for each we may find and a neighborhood such that By varying , we can construct another open cover of using the sets and by compactness there is some such that is a finite cover of , and we can therefore choose . Now for any , we have for some , so by our choice of we have and hence . Finally, let be large enough so that . Then for all , we have and the claim follows.
Proof of path lifting. Since each point of the path has an evenly covered neighborhood (i.e., whose preimage is a disjoint union of open sets, each of which is mapped homeomorphically onto the base neighborhood), our goal is to find a cover of by open sets whose image in is evenly covered. It follows from Claim 4 that we want a natural number such that is evenly covered for all .
- Uniqueness: Suppose we have a lift such that and . We show by induction that is another lift, then .
- Base case: If , then both maps send to .
- Inductive step: Suppose . Then uniqueness follows by applying Claim 3 with , , and taking to be the one-point space.
- Existence: We use induction to construct maps such that each satisfy and , at the end setting .
- Base case: For , we let .
- Inductive step: Suppose has been constructed. Then we may use the existence part of Claim 3 with , , and as the one-point space to construct with precisely the desired properties.
Proof of homotopy lifting
Link to originalHomotopy lifting
Let be a covering map, any topological space and be a homotopy. Let be such that . Then there exists precisely one homotopy with and .
Notes
- Moreover, if is a homotopy relative to a subspace , then so is (suffices to prove a non-relative version).
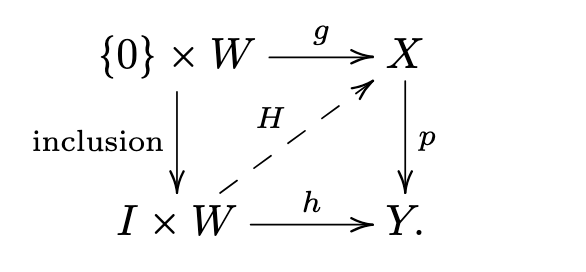
-Path-and-homotopy-lifting/.././attachments/Pasted-image-20250306115149.png)