Universal properties of topologies

Overview §

A universal property of a topology says what data is preserved when restricting a continuous map to that topology.

---

Subspaces §

Theorem: Universal property of the subspace topology

Let $f:X\to Y$ be a function between topological spaces, and $S\subset Y$ be a subset equipped with the subspace topology. If $f(X)\subset S$ and $g:X\to S$ is the function obtained by restricting the codomain of $f$, then $g$ is continuous if an only if $f$ is continuous.

---

Products and disjoint unions §

Theorem: Universal property of the product topology

Let $X,Y,Z$ be topological spaces. If $g:X\to Y$ and $h:X\to Z$ are functions, then the function $f:X\to Y\times Z$ defined by

$$f(x)=(g(x),h(x))$$

is continuous if and only if $f$ and $g$ are. That is, a continuous map to the product $Y\times Z$ is the same data as a pair of continuous maps, one to $Y$ and one to $Z$.

An arbitrary product $\prod X_{\alpha }$ is the “universal” set with the projection maps ${\pi }_{\alpha }:{\prod }_{\alpha }{X}_{\alpha }\to X_{\alpha }$. That is, if $Y$ is a set with the maps $g_{\alpha }:Y\to X_{\alpha }$, there exists a unique $g:Y\to \prod X_{\alpha }$ such that for all $\alpha$, we have ${\pi }_{\alpha }\circ g=g_{\alpha }$.

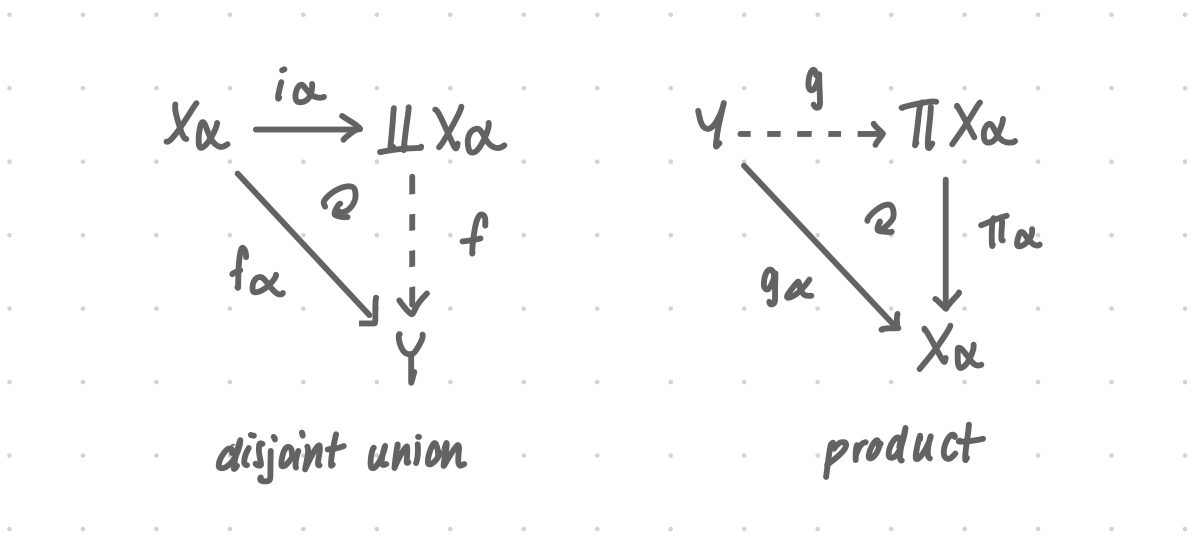
On the other hand, the disjoint union $\coprod X_{\alpha }$ is the “universal” set accepting functions from each $X_{\alpha }$. This means that for any collection of functions $f_{\alpha }:X_{\alpha }\to Y$, there exists a unique function $f:{\coprod }_{\alpha }{X}_{\alpha }\to Y$ such that for all $\alpha$, we have $f\circ i_{\alpha }=f_{\alpha }$.

Theorem: Universal property of the disjoint union

A function between topological spaces $f:X\bigsqcup Y\to Z$ is continuous with respect to the disjoint union if and only if both the restrictions $f{|}_X$ and $f{|}_Y$ are continuous. That is, the function $f$ is the same data as knowing

$$f{|}_X=f\circ i_X:X\to Z\text{and}f{|}_Y=f\circ i_Y:Y\to Z,$$

where $i_Y,i_Z$ is the natural inclusion injection.

#wip Example application HW 6.1, 7.1?

• ${\pi }_1:X\times Y\to X$ closed if $Y$ compact
• $Y$ discrete, then $X\times Y\cong {\coprod }_{y\in Y}{X}_y$.

---

Quotients §

Theorem: Universal property of quotient spaces

If $X$ is a topological space and $\sim$ is an equivalence relation on $X$, the projection map $p:X\to X/\sim$ is continuous.

Moreover, if $f:X\to Y$ is a continuous map that is constant on equivalence classes, meaning that if $x\sim z$, then $f(x)=f(z)$, then $f$ induces a continuous map $\bar{f}:X/\sim \to Y$ defined by

$$\bar{f}([x])=f(x),$$

and $\bar{f}\circ p=f$. We say that $f$ “factors through” the quotient $X/\sim$.

---

Review §

• Check that $f:\prod X_{\alpha }\to Y$ defined above is continuous if and only if each $f_{\alpha }$ is continuous. 🔺