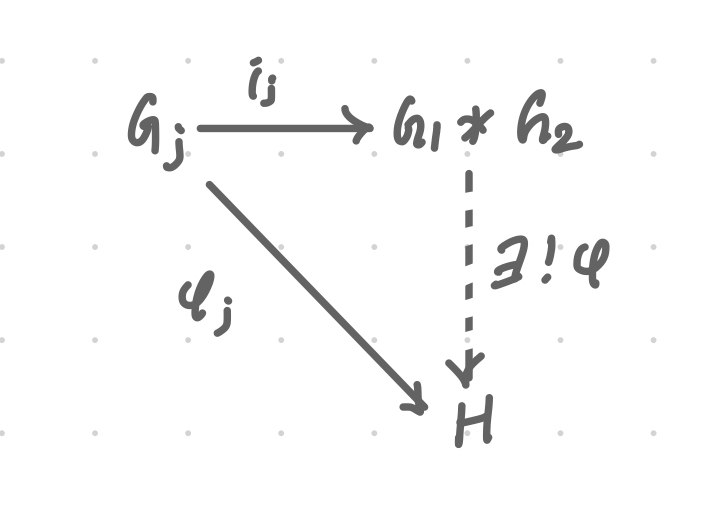Universal properties of groups

See also: Universal properties of topologies

---

Free products

Theorem: Universal property of the free product

Suppose $i_j:G_j\to G_1\ast G_2$ is the inclusion defined by $i_j(g)=g$ for $j=1,2$. Given homomorphisms ${\phi }_j:G_j\to H$, there is a unique homomorphism $\phi :G_1\ast G_2\to H$ defined by

$$\phi (g_1\cdots g_n)={\phi }_{j_1}(g_1)\cdots {\phi }_{j_n}(g_n),$$

where $g_i\in G_{j_i}$ (❓ is a generator?). For an arbitrary product ${\ast }_{j\in J}{G}_j$, this can be also stated as the unique homomorphism $\phi :{\ast }_{j\in J}{G}_j\to H$ such that $\phi {|}_{G_j}=G_j$.

We also have the following restatement of the lemma used to prove (Theorem) The fundamental group of the n-sphere is trivial in higher dimensions, which claimed that given a based loop in a union of spaces has the form of a path concatenation product of based loops from each space.

Theorem (Munkres 59.1): The unique homomorphism of the free product is a surjection

Suppose $X={\bigcup }_{\alpha \in J}{A}_{\alpha }$, where each $A_{\alpha }$ is open and path-connected, and each intersection $A_{\alpha }\cap A_{\beta }$ is also path-connected. For $x_0\in X$, the inclusions $i_{\alpha }:A_{\alpha }\to X$ induce homomorphisms $(i_{\alpha }{)}_{\ast }:{\pi }_1(A_{\alpha },x_0)\to {\pi }_1(X,x_0)$. Consider $G={\pi }_1(X,x_0)$ as the free product with $G_{\alpha }={\pi }_1(A_{\alpha },x_0)$ and homomorphisms ${\phi }_{\alpha }=(i_{\alpha }{)}_{\ast }$. Then $\phi$ is surjective.

wip See 12-3 lecture