Group actions on topological spaces

Overview

Relevant theorems:

• (Theorem) A group acting on a simply connected space is isomorphic to the fundamental group of its orbits

Related notes: Covering maps, Group actions and orbits

---

General group actions in topological spaces

A group action on a topological space $Y$ is a subgroup of the topological symmetries of $Y$—the group of homeomorphisms $\text{Homeo}(Y)$ from a space $Y$ to itself.

Group action on a topological space

If $G$ is a group and $Y$ is any space, a group action $G\times Y\to Y$ is a group homomorphism from $G$ to the group $\text{Homeo}(Y)$ of homeomorphisms from $Y$ to itself. Explicitly, each element of $G$ is associated with a homeomorphism $g:Y\to Y$ with mapping and inverse defined, respectively by

$$y\mapsto g\cdot yy\mapsto g^{-1}\cdot y.$$

Orbits of a group action on a topological space

Given an action of a group $G$ on a space $Y$, the orbit space $Y/G$ of the action is the quotient space formed by identifying $y\sim g\cdot y$. The points of $Y/G$ are the orbits

$$Gy=\{g\cdot y|g\in G\}.$$

---

Continuous actions

Continuous action

Let $G$ be a group and $X$ be a topological space. A continuous (left) action of $G$ on $X$ is a map $\alpha :G\times X\to X$ that is continuous when $G$ is equipped with the discrete topology and also a (left) action on the underlying set, i.e., $\alpha (g_2{g}_1,x)=\alpha (g_2,\alpha (g_1,x))$ for all $g_1,g_2\in G$ and $x\in X$. For simplicity, the action is often written $\alpha (g,x)=g\cdot x$.

Algebraic Topology HW 3.3: Elements in a continuous group action correspond with homeomorphisms

Let $G$ be a group and $\phi :G\to \text{Homeo}(Y)$ be a group homomorphism, where $\text{Homeo}(Y)$ is the group of homeomorphisms $Y\to Y$. Then the mapping $G\times X\to Y$ defined by $(g,y)\mapsto \phi (g)(y)$ is a continuous action of $G$ on $Y$.

Conversely, any continuous action of $G$ on $Y$ arises in this way for a uniquely determined group homomorphism $\phi :G\to \text{Homeo}(Y)$.

Exm

The set of all homeomorphisms $X\to X$ of a space $X$ forms a group with respect to composition, which acts on $X$ in the obvious way: if $f:X\to X$ is a homeomorphism, then $f\cdot x=f(x)$. The subgroup generated by any (finite or infinite) set of homeomorphisms $X\to X$ also acts on $X$ in this way.

---

Covering maps from group actions

• In order to be a covering space, needs to be distinguished locally?

Covering space action

A covering space action $G\times Y\to Y$ is a continuous action of a group $G$ on a space $Y$ such that for all $y\in Y$, there exists a neighborhood $U\subseteq Y$ such that the images for different $g\in G\backslash \{e\}$ are disjoint: $g_1(U)\cap g_2(U)\ne \varnothing ⟹g_1=g_2.$

Lemma

If $G\times Y\to Y$ is a continuous action, then the canonical quotient map $p:Y\to Y/G$ is a covering map if and only if the action is a covering space action.

---

Examples

• The group action $\mathbb{Q}\times \mathbb{R}\to \mathbb{R}$ defined by $(q,t)\mapsto q+t$ is a free action but not a covering. wip is this correct?

Klein bottle

From Algebraic Topology, Homework 3.

Consider the group of transformations generated by the homeomorphisms $S,T:{\mathbb{R}}^2\to {\mathbb{R}}^2$, $S(x,y)=(x+1,-y)T(x,y)=(x,y+1)$ for all $(x,y)\in {\mathbb{R}}^2$: $G=\{g:{\mathbb{R}}^2\to {\mathbb{R}}^2:g\text{ is some composition of }S,T,S^{-1},T^{-1}\}.$

The identity $ST=T{S}^{-1}$ implies any element of $G$ can be written as an element $T^a,S^b$ for $a,b\in \mathbb{Z}$, so the map $\phi :{\mathbb{Z}}^2\to G$ defined by $(a,b)\mapsto T^a{S}^b$ is surjective. After showing that $\phi$ is also injective, we conclude that $\phi$ is a bijection of sets.

The continuous action $G\times {\mathbb{R}}^2\to {\mathbb{R}}^2$ defined by evaluation, i.e., $T^a{S}^b\cdot (x,y)=T^a{X}^b(x,y)$, is in fact a covering space action (e.g., a ball of radius $1/4$ is disjoint from its image).

The quotient space ${\mathbb{R}}^2/G$ is homeomorphic to the Klein bottle since it may be identified with the quotient of the rectangle $[0,1]\times [0,1]$ by the equivalence relation generated by

wip

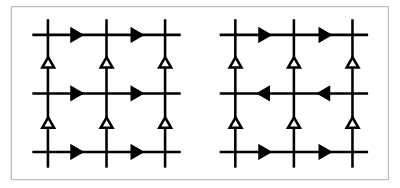Hatecher p. 74