Markov decision processes

Overview

Markov decision processes (MDPs) are a formalism for fully observable, sequential complex decision problems where an agent engages in an extended interaction with the environment. In other words, an MDP is a reinforcement learning task that satisfies the Markov property.

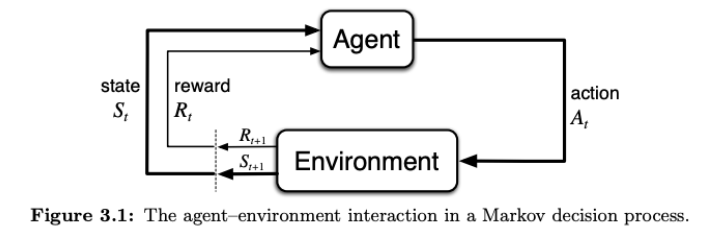
A Markov decision process $(\mathcal{S},\mathcal{A},T,R,\gamma )$ has the following data: a state space $\mathcal{S}$; an action space $\mathcal{A}$; a transition function $T(s’|s,a)$ for how actions in states lead to new states; a reward function $R(s,a,s’)$ which has a value corresponding to each transition; and a discount rate $\gamma \in [0,1]$.

For a given MDP, a policy $\pi$ represents the behavior of a decision-maker by specifying what actions will be taken at each state ¹.

Related notes:

• (Sequential) decision problems
• State and action value functions
• Policy prediction and control
• Bandit problems
• Temporal difference learning

---

Decision policies for actions

Decision policy

Given a Markov decision process $(\mathcal{S},\mathcal{A},T,R,\gamma )$, a policy $\pi$ is a mapping $(s,a)\mapsto \pi (a|s),$ where $\pi (a|s)$ is the probability of taking action $a$ when in state $s$. For example, a deterministic policy is a mapping $\pi :\mathcal{S}\to \mathcal{A}$, while a stochastic policy maps states to action distributions $\pi :\mathcal{S}\to \Delta (\mathcal{A})$.

Trajectory of a MDP, return

Given a Markov decision process with reward function $R(s,a,s’)$ and transition function $T(s’|s,a)$, a single trajectory is a sequence of states, actions, and rewards

$$⟨s_0,a_0,r_0,s_1,a_1,r_1,...⟩,$$

where the reward $r_t=R(s_t,a_t,s_{t+1})$ is defined over a state/action/next-state tuple. The return associated with the trajectory is the discounted cumulative reward

$$G_t=\sum _{t=0}^{\infty }{\gamma }^t{r}_t.$$

---

State reward function

In some cases, such as in the literature on successor representation, the state reward function associated with following policy $\pi$ is denoted $R^{\pi }:\mathcal{S}\to \mathbb{R}$, where $R^{\pi }(s)$ is precisely the expected immediate reward received when in state $s$ and taking actions with probability $\pi (a|s)$.

The expression for $R^{\pi }(s)$ depends on the form of the reward function, as well as whether the policy is deterministic or stochastic:

Reward function form	Deterministic policy $\pi (s)=a$	Stochastic policy $\pi (a\mid s)$
$R:\mathcal{S}\to \mathbb{R}$	$R(s)$	$R(s)$
$R:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$	$R(s,\pi (s))$	${\sum }_a\pi (a\mid s)R(s,a)$
$R:\mathcal{S}\times \mathcal{A}\times \mathcal{S}\to \mathbb{R}$	${\sum }_{s’}T(s’\mid s,a)R(s,a,s’)$	${\sum }_a\pi (a\mid s){\sum }_{s’}T(s’\mid s,a)R(s,a,s’)$

---

Variations

	Single agent	Multi-agent
Fully observable	Markov decision process (MDP)	Stochastic game
Partially observable	Partially observable Markov decision process (POMDP)	Partially observable stochastic game?

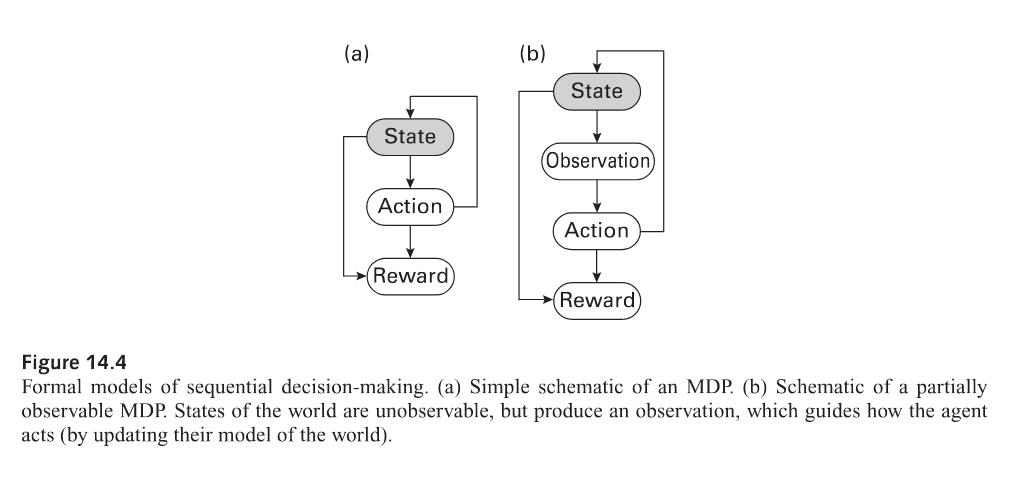
Partially observable MDPs

Multi-agent MDPs with sub-tasks

@2021wuToo

Meta-level MDP

wip @2024griffithsBayesian 331

---

Code snippets

(\mathcal S, \mathcal A, T, R, \gamma)

---

Notes

• @2024griffithsBayesian policy iteration? p. 208
• The MDP framework with differs from a full reinforcement learning setting in that, in the MDP framework, we have general access to the underlying transition probabilities and reward function, and we can examine any state at any time with dynamic programming instead of sampling in sequence. Specifically, in the MDP framework, rewards are given while values are computed or learned; in contrast, the reinforcement learning problem involves trying to find the optimal policy for an MDP in the absence of information about how actions modify states, or what costs or rewards result from an action.

Footnotes

1. In the language of more general sequential decision problems (i.e., in @2025icardResource), this is also known as a stationary strategy, a map from histories to action distributions that depends only on the current state. ↩