Homology of general chain complexes

Overview

A chain complex is a sequence of homomorphisms of abelian groups which generalize singular chains. The homology groups $H_p(C_{\ast },\partial )=\ker ({\partial }_p)/\text{Im}({\partial }_{p+1})$ of a chain complex can be regarded as a measure of non-exactness: the sequence

$$\cdots \to C_{p+1}\to C_p\to C_{p-1}\to \cdots$$

is exact at $C_p$ (i.e., $\ker ({\partial }_p)=\text{Im}({\partial }_{p+1})$) if and only if $H_p(C_{\ast },\partial )=0$.

Homology groups $H_p(X)$ are a result of a two-stage process: forming a chain complex of singular, simplicial, or cellular chains, then taking the homology groups $\ker \partial /\text{Im}\partial$ of this chain complex.

Computations of homology groups typically involve two key theorems, homotopy equivalence and excision.

Relevant theorems:

• (Theorem) A short exact sequence of chain complexes induces a long exact sequence of homology groups
• (Theorem) (Relative) homology is homotopy invariant
• (Theorem) The relative homology of a subset is isomorphic to the subset with excision when the closure of the excision is in the interior of the subset

Related notes:

• Singular chains and singular homology
• Relative singular chains and relative homology
• Reduced singular chains and reduced homology
• Chain homotopies
• Homology with coefficients

---

Chain complexes and chain maps

Chain complex

A chain complex

$$\cdots \to C_{p+1}\to C_p\to C_{p-1}\to \cdots$$

is a sequence consisting of an abelian group $C_p$ and a group homomorphism ${\partial }_p:C_p\to C_{p-1}$ such that ${\partial }_{p-1}\circ {\partial }_p=0$ for all $p\in \mathbb{Z}$ .

The data of all the abelian groups $C_p$ and homomorphisms $\partial$ is often abbreviated $(C_{\ast },\partial )$.

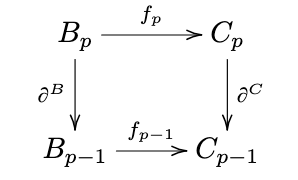
Chain map

Let $(B_{\ast },{\partial }^B)$ and $(C_{\ast },{\partial }^C)$ be chain complexes. A chain map $f_{\ast }:(B_{\ast },{\partial }^B)\to (C_{\ast },{\partial }^C)$ consists of homomorphisms $f_p:B_p\to C_p$ for all $p\in \mathbb{Z}$ which satisfy ${\partial }^C\circ f_p=f_{p-1}\circ {\partial }^B.$

---

Homology groups

Homology groups of a chain complex

If $(C_{\ast },\partial )$ is a chain complex, its homology groups $H_p(C_{\ast },\partial )$ are defined as

$$H_p(C_{\ast },\partial )=\frac{\ker ({\partial }_p:C_p\to C_{p-1})}{\text{Im}({\partial }_{p+1}:C_{p+1}\to C_p)}.$$

Elements of $\ker \partial$ is called cycles, and elements of $\text{Im}\partial$ are called boundaries. If $f:(B_{\ast },\partial )\to (C_{\ast },\partial )$ is a chain map, we define the induced homomorphism $H_p(f):H_p(B_{\ast },\partial )\to H_p(C_{\ast },\partial )$ by

$$[c]\mapsto [f_p(c)]$$

for a cycle $c\in \ker (\partial :B_p\to B_{p-1})$. We often write $f_{\ast }$ for $H_p(f)$.

To see that $f_{\ast }$ is well-defined, we need to justify the following claims:

• The image of any element $f(c)$ is indeed in $\ker (\partial :C_p\to C_{p-1})$: Since $f$ is a chain map, we know that for we have $\partial f(c)=f(\partial c)=0,$ which is zero since $c\in \ker (\partial )$.
• The class $[f(c)]$ does not depend on choice of representative for $[c]$: Suppose $[c]=[d]$, meaning $c,d$ differ by a boundary. In particular, there exists some $x\in C_{p+1}(X)$ such that $d=c+\partial x$. The fact that $f$ consists of group homomorphism implies $f(d)=f(c)+f(\partial x)=f(c)+\partial (f(x)),$ where the second equality again follows from chain map properties. Then $f(c),f(d)$ differ by the boundary $\partial (f(x))$, so $[f(c)]=[f(d)]$.
• The map $f_{\ast }$ is a homomorphism: This follows because every $f_p:B_p\to C_p$ is a homomorphism, so they induce homomorphisms on the quotient.

Transclude of Topological-categories-and-functors#^0c28bf

---

Code snippets

(C_*, \partial)

https://math.stackexchange.com/questions/4399279/short-exact-sequence-of-complexes-induces-long-exact-sequence-of-homology-groups