(Theorem) van Kampen

Overview

The van Kampen theorem is used to compute the fundamental group of a space $X$ that is the union of some open $A,B$ with path-connected intersection. The first “special case” shows that given a point in the intersection $x_0\in A\cap B$, the group ${\pi }_1(X,x_0)$ is generated by the images of the two groups ${\pi }_1(A,x_0)$ and ${\pi }_1(B,x_0)$ under the induced homomorphisms between fundamental groups $(i_j{)}_{\ast }$ induced by inclusion mappings. The van Kampen theorem states that ${\pi }_1(X,x_0)$ is actually completely determined by the two latter groups, the group ${\pi }_1(A\cap B,x_0)$, and the various homomorphisms between fundamental groups induced by inclusion.

---

A special case

Recall the special case of the van Kampen theorem used to prove (Theorem) The fundamental group of the n-sphere is trivial in higher dimensions:

Transclude of (Theorem)-The-fundamental-group-of-the-n-sphere-is-trivial-in-higher-dimensions#^9db065

This can be rephrased in terms of free products as follows:

Lemma: Homomorphism out of the fundamental group of the free product of path-connected spaces is a surjection

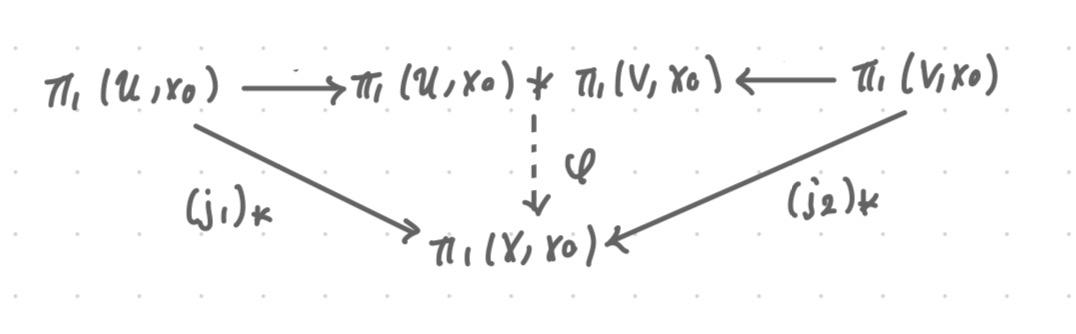
Suppose $X={\bigcup }_{a\in J}{A}_{\alpha }$, where each $A_{\alpha }$ is open and path-connected and the intersections $A_{\alpha }\cap A_{\beta }$ are also path-connected. Let $x_0\in X$ be any point. For each $\alpha \in J$, there exists an inclusion $j_{\alpha }:A_{\alpha }\to X$ which induces a homomorphism between fundamental groups

$$(j_{\alpha }{)}_{\ast }:{\pi }_1(A_{\alpha },x_0)\to {\pi }_1(X,x_0).$$

Setting

$${\phi }_{\alpha }=(j_{\alpha }{)}_{\ast }{G}_{\alpha }={\pi }_1(A_{\alpha },x_0)G={\pi }_1(X,x_0)$$

the unique homomorphism $\phi :{\ast }_{\alpha \in J}{G}_{\alpha }\to G$ out of the free product is a surjection. Equivalently, the images of all $(j_{\alpha }{)}_{\ast }$ generate ${\pi }_1(X,x_0)$.

The homomorphism $\phi$ just concatenates loops, and the previous lemma showed that any $[f]\in {\pi }_1(X,x_0)$ is of the form

$$[f]=[f_1]\ast \cdots \ast [f_k],$$

where $[f_i]\in {\pi }_1(A_{{\alpha }_i},x_0)$.

In particular, $\phi$ works by applying either $(j_1{)}_{\ast }$ or $(j_2{)}_{\ast }$ to some element in the free product, depending on which fundamental group the element originally comes from.

• Corollary: if decomposition both simply connected, intersection path connected, then whole space is simply connected

---

Weak van Kampen

Theorem: Weak van Kampen

If $X=A_1\cup A_2$, each $A_i$ is open and path-connected, $A_1\cap A_2$ is simply connected, and $x_0\in A_1\cap A_2$, then the homomorphism

$$\phi :{\pi }_1(A_1,x_0)\ast {\pi }_1(A_2,x_0)\to {\pi }_1(X,x_0)$$

is an isomorphism.

---

Stronger van Kampen

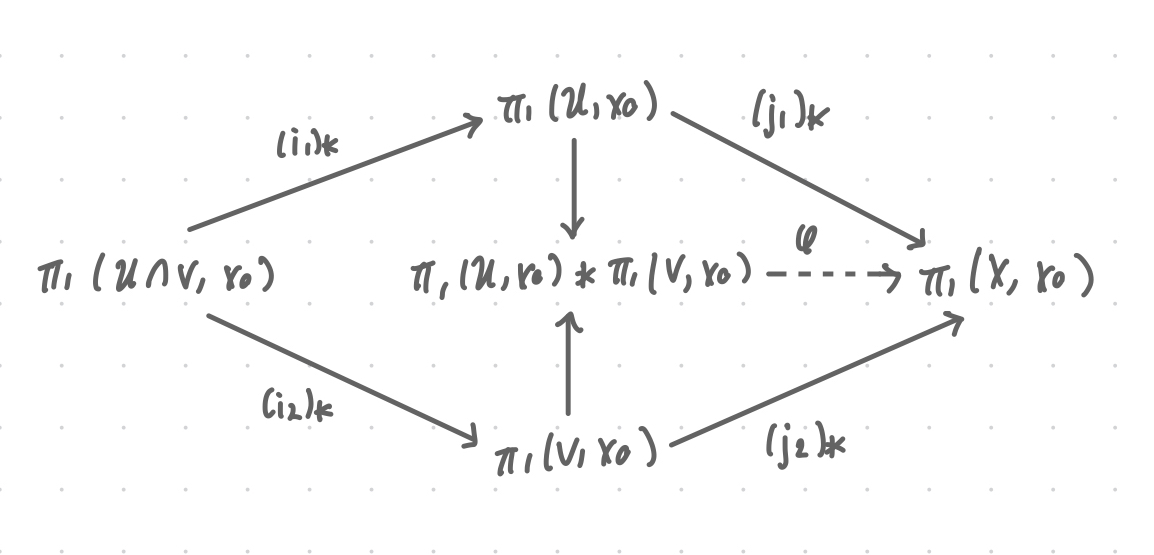
Theorem: Strong van Kampen (statement about the kernel)

Let $X=U\cup V$ where $U,V$ are open and path-connected, $U\cap V$ is path-connected, and $x_0\in U\cap V$. Then the unique homomorphism out of the free product

$$\phi :{\pi }_1(U,x_0)\ast {\pi }_1(V,x_0)\to {\pi }_1(X,x_0)$$

has kernel

$$\ker \phi =⟨⟨\{(i_1{)}_{\ast }^{-1}(g)(i_2{)}_{\ast }(g)|g\in {\pi }_1(U\cap V,x_0)\}⟩⟩,$$

where $(i_1{)}_{\ast }:{\pi }_1(U\cap V,x_0)\to {\pi }_1(U,x_0)$ and $(i_2{)}_{\ast }:{\pi }_1(U\cap V,x_0)\to {\pi }_1(V,x_0)$ are homomorphisms induced by inclusion mappings for the intersection.

Equivalently, the kernel is the smallest normal subgroup containing elements of the form given above. This means precisely that the kernel has all elements $g\in {\pi }_1(U\cap V,x_0)$, plus their conjugations by elements of $U_1,U_2$.

---

Special cases

Intersection of open subsets is simply connected

The weak van Kampen, which requires $U\cap V$ be simply connected, is then a special case of the more general van Kampen theorem where $\phi$ is a isomorphism since its kernel is trivial: if $g\in {\pi }_1(U\cap V,x_0)$, then by definition $g\in 0$, so $\ker \phi =\{e\}$ is generated by the identity only. Since $\phi$ is a surjection, it follows from (Theorem) First isomorphism theorem that

$$\text{im}\phi ={\pi }_1(X,x_0)\cong {\pi }_1(U,x_0)\ast {\pi }_1(V,x_0)/\ker \phi ={\pi }_1(U,x_0)\ast {\pi }_1(V,x_0).$$

One of the open subsets is simply connected

Suppose $U$ is simply connected. Then $\ker \phi$ is generated by the set

$$\{(i_2{)}_{\ast }(g)|g\in {\pi }_1(U\cap V,x_0\}=\{\text{image of }(i_2{)}_{\ast }:{\pi }_1(U\cap V,x_0)\to {\pi }_1(V,x_0)\},$$

as $(i_1{)}_{\ast }^{-1}(g)\in {\pi }_1(U,x_0)=\{e\}$ is simply the identity element, and we have precisely

$${\pi }_1(X,x_0)\cong \frac{{\pi }_1(V,x_0)}{⟨⟨(i_2{)}_{\ast }({\pi }_1(V,x_0))⟩⟩}.$$

---

Examples and computations

A general strategy for constructing open sets $U,V$ that satisfy the hypotheses of van Kampen is to take some sets you think they “should be,” then make them to be a little bigger to be open and cover the space $X$. For example, when $X=S^1\vee S^1$, we can take $U,V$ to be copies of $S^1$ with a small open neighborhood about the point that they meet at. Similarly, if $X$ is some surface constructed by “gluing” edges to make a polygon $P$ (e.g., the torus $S^1\times S^1$ constructed from the square, or the genus-2 torus ${\sum }_2$ constructed from the octagon), one can take $U=P\backslash \{p\}$ with some point removed and $V$ to be a neighborhood about $p\in P$.

Simply connected intersection: The figure 8

Given $X=S^1\vee S^1$, recall that the $\vee$ operation denotes the two copies of $S^1$ that intersect at a single point. Take $A_i$ to be one copy of $S^1$ together with a neighborhood of $x_0$ (this looks like a circle with an arc stuck to it). We know ${\pi }_1(A_i)\cong \mathbb{Z}$ for $i=1,2$, since each $A_i$ is homotopy equivalent to $S^1$ ($A_i$ deformation retracts onto $S^1$) and the fundamental group is invariant under homotopy equivalence. Further $A_1\cap A_2$ (this looks like a curved cross) deformation retracts onto the single point $x_0$, so they have isomorphic fundamental groups

$${\pi }_1(A_1\cap A_2,x_0)\cong {\pi }_1(x_0,x_0)=0$$

and $A_1\cap A_2$ is simply connected. Then the weak van Kampen implies ${\pi }_1(X,x_0)\cong \mathbb{Z}\ast \mathbb{Z}=F_2$, the free product of rank 2.

By induction, the fundamental group of $n$ circles meeting at a single point is isomorphic to $F_n$, the free product of rank $n$.

One simply connected subspace: $S^1\times S^1$

The torus $T=S^1\times S^1$, considered as a quotient of the square, can be decomposed into the following: let $A_1$ be the filled square with a point removed, and let $A_2$ be a basic open neighborhood of that point. Then we have the following:

• $A_1$ has a deformation retraction to the boundary of the square, which has two pairs of sides $a,b$ with the same orientation. This is homeomorphic to $S^1\vee S^1$, so ${\pi }_1(A_1)=\mathbb{Z}\ast \mathbb{Z}$ and is generated by $a,b$.
• $A_2$ is simply connected, so ${\pi }_1(A_2)=0$.
• $A_1\cap A_2$ is homeomorphic to the annulus, which can be retracted to $S^1$ and therefore has ${\pi }_1(A_1\cap A_2)\cong \mathbb{Z}$, which is generated by a single loop $\omega$ about the circle.

The induced homomorphism ${\pi }_1(A_1\cap A_2)\to {\pi }_1(A_1)$ maps $\omega \mapsto ab{a}^{-1}{b}^{-1}$; informally, the loop $\omega$ is embedded as a loop around the hole in $A_1$, which is homotopic to the commutator of the generators $a,b$. Thus, van Kampen implies

$${\pi }_1(T)\cong \frac{\mathbb{Z}\ast \mathbb{Z}}{⟨⟨ab{a}^{-1}{b}^{-1}⟩⟩}\cong ⟨a,b|ab{a}^{-1}{b}^{-1}=1⟩$$

The generators $a,b$ commute, so this is precisely the presentation of the abelian group $\mathbb{Z}\times \mathbb{Z}$.

Notes

2025-02-13

• Alternative statement of the first lemma from Algebraic Topology

Lemma: van Kampen lite

If $X={\bigcup }_{\alpha }{U}_{\alpha }$ is an open cover such that the intersection $U_{\alpha }\cap U_{\beta }$ is path-connected for all $\alpha ,\beta$ and there is some $x_0\in U_{\alpha }$ for all $\alpha$, then ${\pi }_1(X,x_0)$ is generated by ${\bigcup }_{\alpha }\text{Im}((i_{\alpha }{)}_{\ast }:{\pi }_1(U_{\alpha },x_0)\to {\pi }_1(X,x_0)),$ the union of the images of all homomorphisms induced by inclusion mappings $i_{\alpha }:U_{\alpha }\to X$.

• Circle – decompose into streographic projections