Overview
Turing machines are computational systems that give a mathematical precisification of “human effectively computable” formulas—an intuitive notion—that are expressed in formal systems. A Turing machine has three components: an infinite (equivalently, unbounded) memory tape, a read/write “head,” and a control unit with a set of instructions.
The Church-Turing thesis is the (falsifiable) claim that computability proofs for any formal system can be proven using Turing machines: “If an algorithm exists, then there exists a Turing machine to perform that algorithm.”
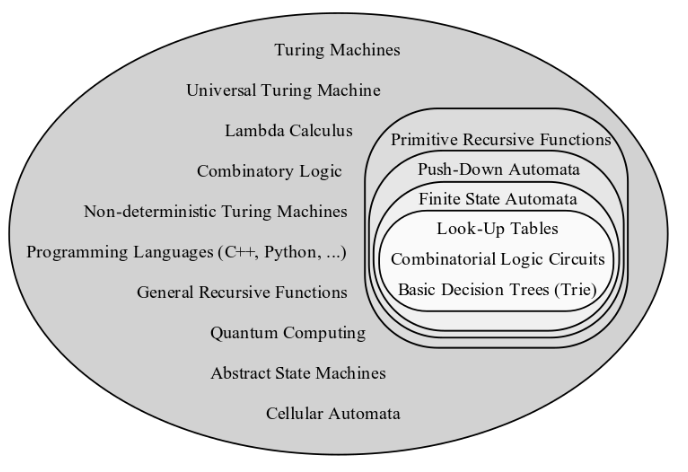
A general set of data-manipulation rules is called Turing complete if it can be used to simulate any Turing machine—if it is at least as powerful as a Turing machine. On the other hand, a Turing-complete system is called Turing equivalent if it computes precisely the same class of functions as a Turing machine—if it is exactly as powerful as a Turing machine. We say a computation system is universal or has universal scope if and only if it can simulate any Turing machine.
Related notes:
- Chomsky hierarchy of computation systems
- Undecidability and incompleteness theorems
- Effectively calculable, recursive, and computable are equivalent descriptions of functions
- Combinatory logic and lambda-calculus
A semi-formal definition
@2025icardResource 9: Turing machine
A Turing machine is given by:
- (i) An infinite read/write tape with inputs (“observations”) written on the tape at the beginning of computation, and outputs (“actions”) written on the tape at the time of halting;
- (ii) A “random bit” tape with an infinite binary sequence, each bit assumed to be drawn uniformly and independently with probability 0.5;
- (iii) A finite set of states that the machine can be in;
- (iv) Transition rules of the form , which can be stated as follows: when in state , reading symbol and random bit , rewrite as , go direction on the tape (left or right), and enter state .
A Turing machine is said to be deterministic if its actions do not depend on the input (ii). Deterministic Turing machines define exactly the computable functions.
Turing completeness and equivalence
In order to be Turing-equivalent, a computer must have unbounded memory. From Akhlaghpour (2020):
Turing-equivalence is precisely what you get when you ask the question: what is the most powerful scope of computation that finite physical devices can achieve? To consider them as infinite or physically unrealistic is deeply mistaken and obscures the classical insights from the theory of computation.
Abstract systems that can compute any computable function, such as Turing machines, are also said to have universal scope.
Relation to cognition and intelligence
Turing machines minimize Intelligence during computation, so that explanations of computational ability don’t have to appeal to some other substrate (e.g., appeal to strong emergence). Recognition and discernment is the only trace of intelligence in a Turing machine, after Dennett.
Relation to formal limitations
Hilbert’s Entscheidungsproblem
Is there an algorithm that can decide whether any given statement (e.g., a mathematical statement) in a sufficiently rich formal system is true or false?
Highlights
- Requirements for finite state machines and Turing machines—mathematical abstractions—to be physically realized: “Finite state machines are no less of a mathematical abstraction than Turing machines are. And both are relevant to studying the real world. You can implement a finite state machine by creating something that recruits more energy when needed. Similarly, you can implement a Turing-equivalent machine by creating something that recruits more memory space [and energy] when needed. The fact that both of these will eventually hit some limit does not make them physically unrealizable.”
- Turing machines use finite means: “Minsky explains that “instead of an infinite tape, we need only an inexhaustible tape factory” and that “this picture gives a reassuringly finite picture [of Turing machines]“.”
Notes
- Dennett: “competence without comprehension”
A Turing machine has three components: the infinite tape, a “read/write head,” and a control unit, which is a set of instructions.
- Style of computation that involves algorithms over explicit symbols (Luke still thinks this is basis of intelligence)
- A finite state machine that has read/write memory
- Things that don’t allow the Turing Machine to compute anything new (add computational power)
- Probabilistic Chomsky hierarchy? – non-deterministic state changes
- Von Neumann combines I/O and program
References
- @1936turingOn, “On computable numbers”
- Akhlaghpour (2020), “Can a finite physical device be Turing-equivalent?
- @2022akhlaghpourRNABased, “An RNA-based theory of natural universal computation”