Markov decision processes and dynamic programming

Overview

Markov decision processes (MDPs) are a formalism for fully observable, sequential complex decision problems where an agent engages in an extended interaction with the environment.

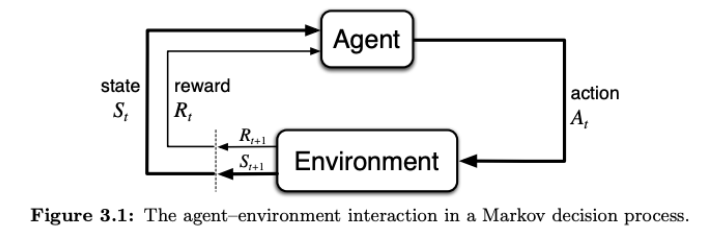
A Markov decision process $(\mathcal{S},\mathcal{A},T,R,\gamma )$ has the following data: a state space $\mathcal{S}$; an action space $\mathcal{A}$; a transition function $T(s’|s,a)$ for how actions in states lead to new states; a reward function $R(s,a,s’)$ which has a value corresponding to each transition; and a discount rate $\gamma \in [0,1]$.

For a given MDP, a policy $\pi$ represents the behavior of a decision-maker by specifying what actions will be taken at each state. Policy prediction or evaluation involves calculating the expected return from a fixed policy, while policy control involves selecting the optimal policy based on the highest expected reward.

Related notes:

• Bandits, exploration, and exploitation
• Temporal difference learning

---

Key terms

• Policy: a formalization of agent behavior as a function $\mathcal{S}\to \mathcal{A}$ mapping states to actions.
• Prediction: also known as policy evaluation; the computational problem of determining how much long-term reward would be obtained given a policy and an initial state.
• Value: a standard method of defining long-term reward as the expected cumulative discounted infinite sum of rewards. In contrast to reward, value is derived from a combination of rewards, the environment, and future behaviors.
• Optimal control: also known as policy optimization; the computational problem of finding the policy with the maximal value function given an MDP. Using the standard definition of value above, there is a unique optimal value function expressed in terms of Bellman optimality equations.
• Planning: the control problem with a known reward and transition model.
• Dynamic programming: in this context, a class of algorithms that, given the full state space, calculates the value function via backward induction. wip
• Value iteration: the dynamic programming algorithm for optimal control.

---

Policies and value functions

Decision policy, value

Given a Markov decision process $(\mathcal{S},\mathcal{A},T,R,\gamma )$, a policy $\pi$ represents the behavior of a decision-maker by specifying what actions will be taken at each state. For example, a deterministic policy is a mapping $\pi :\mathcal{S}\to \mathcal{A}$, while a stochastic policy maps states to action distributions $\pi :\mathcal{S}\to \Delta (\mathcal{A})$.

The value of a policy $\pi$ from a state $s_0$ is the expected cumulative, discounted reward that results from following $\pi$.

Trajectory of a MDP, return

Given a Markov decision process with reward function $R(s,a,s’)$ and transition function $T(s’|s,a)$, a single trajectory is a sequence of states, actions, and rewards

$$⟨s_0,a_0,r_0,s_1,a_1,r_1,...⟩,$$

where the reward $r_t=R(s_t,a_t,s_{t+1})$ is defined over a state/action/next-state tuple. The return associated with the trajectory is the discounted cumulative reward

$$\sum _{t=0}^{\infty }{\gamma }^t{r}_t.$$

---

Policy prediction

The policy prediction problem is to calculate the state value function, or expected return, from every state that results from following a fixed policy $\pi$.

Equation: State value

The value of a state $s$ under policy $\pi$ is given by the expected return (i.e., cumulative discounted reward) conditioned on starting at state $s_0=s$ and following $\pi$ thereafter:

$$v_{\pi }(s)={\mathbb{E}}_{\pi ,T}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t\mid s_0=s\right],$$

where $r_t=R(s_t,a_t,s_{t+1})$ is the reward at $t$ with action given by the policy $a_t\sim \pi (\cdot |s_t)$ and next state given by transition dynamics $s_{t+1}\sim T(\cdot |s_t,a_t)$, and $\gamma \in (0,1]$ is the discount rate.

The Monte Carlo policy prediction algorithm calculates $v_{\pi }$ by repeatedly sampling trajectories and averaging returns.

Algorithm: Monte Carlo policy prediction

Input: A policy $\pi$ to evaluate and a state $s$ to evaluate from.

• Initialize the return $G=0$ and timestep $t=0$
• While $s$ is not an absorbing state (a state that always leads to itself regardless of what action is taken, and always returns a reward of $0$):
  • Sample action $a\sim \pi (a|s)$
  • Sample next state $s’\sim T(s’|s,a)$
  • Calculate reward $r=R(s,a,s’)$
  • Update $G\leftarrow G+{\gamma }^t\cdot r$
  • Update $s\leftarrow s’$
• Return $G$

On the other hand, discounted infinite horizon MDPs have the property that $v_{\pi }$ can be expressed with a set of primitive recursive equations. This allows for calculating calculating exact values using dynamic programming: the general idea is to initialize the value function $v_{\pi }(s)$ arbitrarily, then use the right-hand expression to calculate updated value functions until the function stops changing and Bellman’s equations are satisfied.

Equation: Bellman’s equation

$$v_{\pi }(s)=\sum _{a,s^{\prime }}\pi (a|s)T(s^{\prime }|s,a)\left[R(s,a,s^{\prime })+\gamma v_{\pi }(s^{\prime })\right]$$

Algorithm: Bellman policy prediction

Input: A policy $\pi$, a MDP $(\mathcal{S},\mathcal{A},T,R,\gamma )$, and a convergence precision ${\Delta }_{max}$.

• Initialize $v_{\pi }(s)=0$ for all $s\in \mathcal{S}$
• For $i$ in $\{1,2,\dots ,n_{maxiters}\}$:
  • $\Delta =0$
  • For $s\in \mathcal{S}$:
    • If $s$ is an absorbing state:
      • Skip
    • $v_{new}\leftarrow {\sum }_{a,s’}\pi (a|s)T(s’|s,a)[R(s,a,s’)+\gamma v_{\pi }(s’)]$
    • $\Delta =\text{max}(\Delta ,|v_{\pi }(s)-v_{new}|)$
    • $v_{\pi }(s)\leftarrow v_{new}$
  • If $\Delta <{\Delta }_{max}$:
    • Break
• Return $\{v_{\pi }(s){\}}_{s\in \mathcal{S}}$

---

Policy control

Policy control is the problem of calculating the optimal policy, which can again be computed recursively. Rather than selecting an action according to a policy $\pi$, the Bellman optimality equations express selecting the best action in terms of state values. Like before, we have an iterative algorithm that converges on a $v_{\ast }$ satisfying these equations.

Equation: Bellman optimality equations

$$v_{\ast }(s)=\underset{a}{\max }\left\{\sum _{s^{\prime }}T(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma v_{\ast }(s^{\prime })]\right\}$$

Algorithm: Value iteration

Input: An MDP $(\mathcal{S},\mathcal{A},T,R,\gamma )$ and a convergence precision ${\Delta }_{max}$.

• Initialize $v_{\ast }(s)=0$ for all $s\in \mathcal{S}$.
• For $i$ in $\{1,2,\dots ,n_{maxiters}$:
  • $\Delta =0$
  • For $s\in \mathcal{S}$:
    • If $s$ is absorbing:
      • Skip
    • $v_{new}\leftarrow {\max }_a{\sum }_{s^{\prime }}T(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma v_{\ast }(s^{\prime })]$
    • $\Delta =\max (\Delta ,|v_{\ast }(s)-v_{new})$
    • $v_{\ast }(s)\leftarrow v_{new}$
  • If $\Delta <{\Delta }_{max}$:
    • Break
• Return $\{v_{\ast }(s){\}}_{s\in \mathcal{S}}$

Given $v_{\ast },R,T$, the optimal policy can be calculated by calculating the optimal state action values for each action in a state, then taking the best action(s). In particular, we have the $Q$-value (for “quality”) of an action $a$ taken at a state $s$ assuming that we will act optimally from then on.

Equation: $Q$-value

$$q_{\ast }(s,a)=\sum _{s^{\prime }}T(s^{\prime }|s,a)[R(s,a,s^{\prime })+\gamma v_{\ast }(s^{\prime })]$$

The optimal stochastic policy is then any policy that is greedy with respect to the optimal $Q$-values, meaning it is uniform over all actions equal to the maximum value ¹:

$${\pi }_{\ast }(a|s)\propto 1[q_{\ast }(s,a)=\underset{b}{\max }q(s,b)],$$

where $1[P]=1$ if $P$ is true and $0$ otherwise, thus ${\sum }_a{\pi }_{\ast }(a|s)=1$ normalizes to a probability distribution.

---

Variations

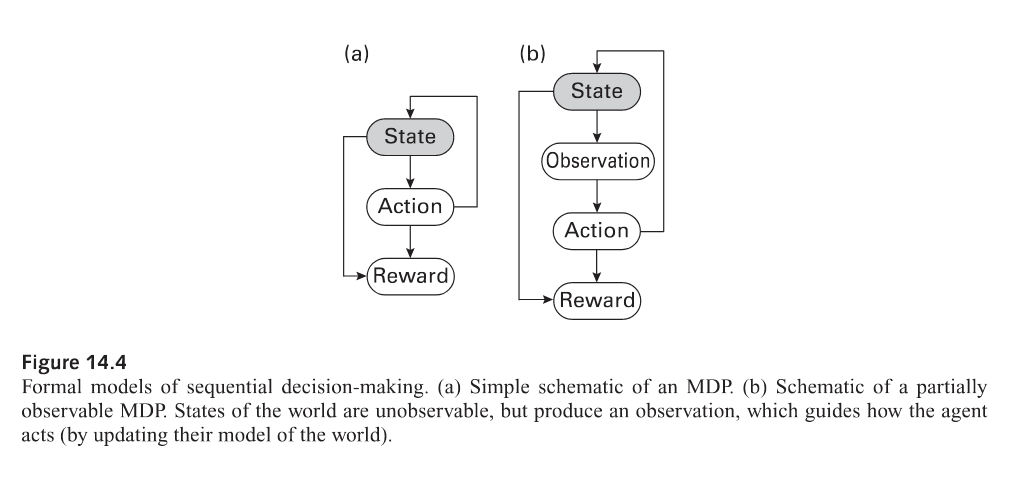
Partially observable MDPs

Stochastic games

@2016hoFeaturebased

Multi-agent MDPs

@2020carrollUtility

Multi-agent MDPs with sub-tasks

@2021wuToo

Meta-level MDP

wip @2024griffithsBayesian 331

---

Code snippets

(\mathcal S, \mathcal A, T, R, \gamma)

---

Notes

• @2024griffithsBayesian policy iteration? p. 208
• The MDP framework with differs from a full reinforcement learning setting in that, in the MDP framework, we have general access to the underlying transition probabilities and reward function, and we can examine any state at any time with dynamic programming instead of sampling in sequence. Specifically, in the MDP framework, rewards are given while values are computed or learned; in contrast, the reinforcement learning problem involves trying to find the optimal policy for an MDP in the absence of information about how actions modify states, or what costs or rewards result from an action.

Footnotes

1. For example, if there is only one maximum value, then the policy is deterministic. ↩